12. 군집화(Clustering)

Index

군집분석은 대표적인 머신러닝의 비지도 학습이다. 머신러닝의 분류/회귀와 같이 직접적인 예측을 수행하는 알고리즘은 아니지만, 데이터의 탐색단계 (EDA)에서 데이터간의 군집/패턴등을 시각화하고 이해하는데 유용하고 (이상탐지에도 쓰일 수 있겠다) 전처리 단계에서도 사용될 수 있는데, 예를들어 데이터셋이 우리가 알지 못했던 명확한 특성을 가진 몇가지 군집으로 분류된다면 각 군집별로 개별적인 머신러닝/딥러닝 모델을 학습시키는게 효율적일 수 있다. 

이번 포스팅에서는 Clustering의 대표적인 모델  4가지에 대해서, 그리고 정답이 따로 없는 군집화 모델들에 대한 평가 방법에 대해 정리한다.

 

군집화의 대표적인 모델 

 

1. K-means Clustering 

• 군집화의 가장 대표적이고 간결한 알고리즘
• 군집의 중심점(Centroid)이라는 특정한 지점을 선택해 해당 중심에 가까운 포인트를 선택하여 군집화하는 방법
• K-means는 원형의 범위를 가질수록 효율이 높다. (데이터가 길쭉한 타원형으로 늘어선 경우에 성능이 떨어짐)
• 군집화 프로세스 
  1. k개의 초기 중심점을 선택
  2. 각 데이터는 가장 가까운 중심점에 소속됨
  3. 각 중심점을 소속된 데이터 집합의 중심으로 이동 
  4. 이동된 중심점 기준으로 2번3번을 반복 
  5. 중심점이 움직이지 않으면 군집화 종료

• 단점: ① 속성의 개수가 많을수록 성능/속도 ↓ (사전 PCA필요) ② 군집의 개수(k) 선택이 어려움/모호함
• 사이킷런의 Kmeans 모듈을 활용한 코드구현
  
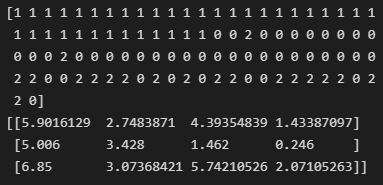
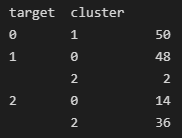
  1. 주요 파라미터: n_cluster = 중심점 개수, init = 중심점 초기화설정방법, max_iter = 최대반복회수
  2. 주요 (반환)속성: labels = 각 데이터가 속한 군집 중심점 레이블, cluster_centers_ = 각 중심점의 좌표

    from sklearn.cluster import KMeans

                                                                                                               

    kmeans = KMeans(n_clusters=3, init='k-means++', max_iter=300,random_state=0)                   ↓ print 출력결과 

    

kmeans.fit(irisDF)  #

 

    print(kmeans.labels_)

    print(kmeans.cluster_centers_)

 

    # 군집 결과를 DataFrame에 추가한뒤 타겟/군집별 개수세기 

    irisDF['target'] = iris.target

    irisDF['cluster']=kmeans.labels_

    iris_result = irisDF.groupby(['target','cluster'])['sepal_width'].count()

    print(iris_result)

 

                                                                                               

 

2. Mean Shift

• K-means 와 같이 중심을 계속 이동시켜가며 군집화 하는데, K-means가 거리기반으로 이동했다면, Mean shift는 밀도가 가장 높은곳으로 이동한다.
• 밀도를 찾기위해 확률밀도함수를 사용한다. 
• 개별 데이터로 주변 데이터와의 거리값을 KDE(Kernel Density Estimation)을 이용해 확률밀도함수를 찾는다.
• 모든 데이터에 대해서, 확률밀도 함수의 피크점 (=거리의 분포가 가장 높은곳)으로 이동
• 지정된 횟수만큼 이동후에 개별 데이터들이 모인 중심점을 군집중심으로 설정한다. → Mean shift 방식은 군집의 개수를 사전에 지정하지 않고, 대역폭(h)에 따라 정해진다 (h가 클수록 작은군집개수, h가 작을수록 뾰족하고, overfit 잘됨)

※ KDE (Kernerl Density Estimation) 는 non-parametric 한 밀도추정 방식. (parametric = 데이터가 특정 확률분포를 따를것이라 가정하고 파라미터만 추정) 

- 개별 관측 데이터에 커널함수(ex.가우시안 분포함수 커널)를 적용하고, 이 적용된 값을 모두 더한뒤 데이터 레코드수로 나누어 확률밀도함수를 추정 (오른쪽 위 그림예시)

- 대역폭 h로 확률밀도함수의 모양을 컨트롤하는데, h가 클수록 평활화(smoothing)된다. 

 

• Meanshift 군집화 코드예시. 대역폭h 를 bandwidth 파라미터로 컨트롤한다. h가 너무크면 군집을 너무 적게, 너무작으면 군집을 너무 많이 분류하는 경향이 있다. 그래서 estimate_bandwidth 라는 매서드를 활용해 최적의 h를 넣는다. 

   

    from sklearn.cluster import MeanShift

    from sklearn.cluster import estimate_bandwidth

    X, y = make_blobs(n_samples=200, n_features=2, centers=3,

                    cluster_std=0.7, random_state=0)

 

    best_bandwidth = estimate_bandwidth(X)

 

    meanshift= MeanShift(bandwidth=best_bandwidth)

 

    cluster_labels = meanshift.fit_predict(X)

    print('cluster labels 유형:', np.unique(cluster_labels))

 

 

3. Gaussian Mixture Model (GMM) 

• GMM 은 대상 데이터가 가우시안 분포를 따른다고 가정하고(따라서 parametric model), 개별 가우시안 분포의 선형결합으로 만들어진 분포에서 개별 가우시안 분포를 확률적으로 추정하는 방법이다. 
• K-means는 거리기반, Mean shift는 밀도기반이라면 GMM 은 확률기반
• GMM은 2가지 모수추정을 한다. ①개별 정규분포들의 평균과 분산 ②각 데이터가 어떤 정규분포에 해당할지 확률

•  수식으로 보면 아래와 같이 K개의 서로다른 다변량 가우시안 분포N(x)가 mixing coeffiecient(π)에 의해 선형결합된 형태로, μ Σ π 3가지 모수가 추정대상이다. 

• 3개 모수를 추정하기위해 EM(Expectation and Maximization)방법을 적용하는데, 사이킷런의 GaussianMixture 모듈을 활용하면 내장되어있다. 군집의개수 n_components 는 사전에 지정해줘야한다. 

from sklearn.mixture import GaussianMixture

gmm = GaussianMixture(n_components=3, random_state=0).fit(iris.data)

gmm_cluster_labels = gmm.predict(iris.data)

 

4. DBSCAN (Density Based Spatial Clustering of Application with Noise) 

• 간단하고 직관적이면서, 데이터 분포가 기하학적으로 복잡한 데이터에도 효과적이다. 
• 군집의 개수를 사전에 지정하지 않는다. 
• DBSCAN의 중요 파라미터 ①입실론 영역(eps, 일반적으로 1이하) ②핵심 포인트의 데이터 최소 포함개수 기준
• DBSCAN은 밀도와 거리를 둘다 고려하는 방식으로 군집화 프로세스는 아래와 같다.

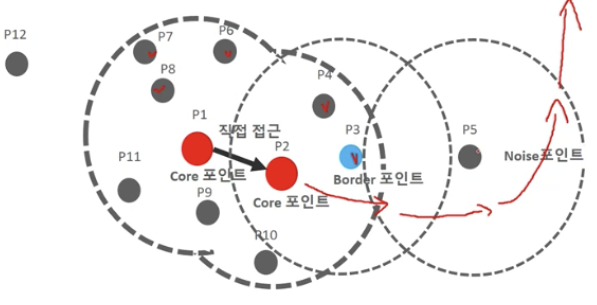
• 각 데이터는 일정 반경(입실론)안에 최소 데이터 개수를 만족하는지, 핵심포인트를 포함하는지 여부로 아래와 같이 3가지 종류로 분류한다(이웃포인트 제외). 이후, 핵신포인트들의 입실론 영역을 연결해 가면서 군집화 한다. 
  1. 이웃 포인트: 입실론 안에 자신이 아닌 포인트들
  2. 핵심 포인트: 입실론 안에 최소개수 이상의 데이터 보유 
  3. 경계 포인트: 입실론 안에 최소개수 이상의 데이터가 없지만 핵심포인트를 이웃포인트로 보유한 것 
  4. 잡음 포인트: 핵심도 아니고 경계도 아닌 포인트

• DBSCAN 은 군집 레이블을 0,1,2... 외에 -1도 반환하는데, -1 이 noise 군집이다. 
• 코드예시, eps(입실론 반경크기)를 늘릴수록 노이즈는 적어지고, min_samples 개수는 늘릴수록 노이즈가 많아진다.

    from sklearn.cluster import DBSCAN

    dbscan = DBSCAN(eps=0.6, min_samples=8, metric='euclidean')

    dbscan_labels = dbscan.fit_predict(iris.data)

 

군집 평가 (Cluster Evaluation)

지도학습의 경우 분류모델에서는 오차행렬을 통한 정확도,정밀도,재현율 등의 지표 혹은 Cross entropy등을 사용해 학습모델을 평가했고, 회귀모델에서는 MSE,MAE,R^ 등 추정값과 실제값 차이에 대한 비용함수로 모델을 평가했다. 

군집화 모델도 위에서 다뤘던 여러가지 파라미터(군집개수, 입실론, 대역폭 등)들의 최적화를 위해 어느정도의 평가가 필요한데 지도학습에서 사용한 label기반의 평가지표들을 사용할 수 없다. 

따라서 비지도학습에 해당하는 군집화 모델에서 주로 사용하는 '실루엣 분석' 을 중심으로 군집평가에 대해 정리한다. 

 

실루엣 분석

• 각 군집이 얼마나 효율적으로 분리됬는가: 다른 군집과 거리가 멀고, 동일 군집간 거리가 가까운 정도
• 실루엣 계수: 자신과 가장 가까운 군집과의 거리와 자신이 속합 군집간의 거리의 차이로 계산되며, 1에 가까울수록 좋다. (자기 군집과 가깝고 근처 군집과 멀다는 의미)  
• 실루엣 분석은 개별 데이터별로 계산을 하기 때문에 메모리 부하가 크다. → 데이터가 크면 군집별 임의 데이터 샘플링 해 평가하는 방법 등 고민이 필요하다. 

• 개별 군집의 실루엣 계수 평균값이, 전체 실루엣 계수 평균값에서 크게 벗어나지 않는 것이 좋다. (특정 군집의 실루엣 평균만 좋은 상황은 Bad)
• 사이킷런의 silhouette_samples, silhouette_score 모듈을 이용해 실루엣 계수 계산 

  from sklearn.metrics import silhouette_samples, silhouette_score

  # iris 의 모든 개별 데이터에 실루엣 계수값을 구함.irisDF['cluster'] 는 K-means를 통해 구한 군집번호

  score_samples = silhouette_samples(iris.data, irisDF['cluster'])

  irisDF['silhouette_coeff'] = score_samples

  # 모든 데이터의 평균 실루엣 계수값을 구함.

  average_score = silhouette_score(iris.data, irisDF['cluster'])

  print('붓꽃 데이터셋 Silhouette Analysis Score:{0:.3f}'.format(average_score))

• 아래와 같이 cluster 별 실루엣 계수비교 가능, (아래 예시는 1번 군집만 계수가 높은 안좋은 상황) 

  irisDF.groupby('cluster')['silhouette_coeff'].mean()

 

실루엣 계수의 시각화와 군집개수 최적화 

    ### 여러개의 클러스터링 갯수를 List로 입력 받아 각각의 실루엣 계수를 면적으로 시각화한 함수 작성

    def visualize_silhouette(cluster_lists, X_features):

       

        from sklearn.cluster import KMeans

        from sklearn.metrics import silhouette_samples, silhouette_score

        import matplotlib.cm as cm

        import math

       

        # 입력값으로 클러스터링 갯수들을 리스트로 받아서, 각 갯수별로 클러스터링을 적용하고 실루엣 개수를 구함

        n_cols = len(cluster_lists)

       

        # plt.subplots()으로 리스트에 기재된 클러스터링 수만큼의 sub figures를 가지는 axs 생성

        fig, axs = plt.subplots(figsize=(4*n_cols, 4), nrows=1, ncols=n_cols)

       

        # 리스트에 기재된 클러스터링 갯수들을 차례로 iteration 수행하면서 실루엣 개수 시각화

        for ind, n_cluster in enumerate(cluster_lists):

           

            # KMeans 클러스터링 수행하고, 실루엣 스코어와 개별 데이터의 실루엣 값 계산.

            clusterer = KMeans(n_clusters = n_cluster, max_iter=500, random_state=0)

            cluster_labels = clusterer.fit_predict(X_features)

           

            sil_avg = silhouette_score(X_features, cluster_labels)

            sil_values = silhouette_samples(X_features, cluster_labels)

           

            y_lower = 10

            axs[ind].set_title('Number of Cluster : '+ str(n_cluster)+'\n' \

                            'Silhouette Score :' + str(round(sil_avg,3)) )

            axs[ind].set_xlabel("The silhouette coefficient values")

            axs[ind].set_ylabel("Cluster label")

            axs[ind].set_xlim([-0.1, 1])

            axs[ind].set_ylim([0, len(X_features) + (n_cluster + 1) * 10])

            axs[ind].set_yticks([])  # Clear the yaxis labels / ticks

            axs[ind].set_xticks([0, 0.2, 0.4, 0.6, 0.8, 1])

           

            # 클러스터링 갯수별로 fill_betweenx( )형태의 막대 그래프 표현.

            for i in range(n_cluster):

                ith_cluster_sil_values = sil_values[cluster_labels==i]

                ith_cluster_sil_values.sort()

               

                size_cluster_i = ith_cluster_sil_values.shape[0]

                y_upper = y_lower + size_cluster_i

               

                color = cm.nipy_spectral(float(i) / n_cluster)

                axs[ind].fill_betweenx(np.arange(y_lower, y_upper), 0, ith_cluster_sil_values, \

                                    facecolor=color, edgecolor=color, alpha=0.7)

                axs[ind].text(-0.05, y_lower + 0.5 * size_cluster_i, str(i))

                y_lower = y_upper + 10

               

            axs[ind].axvline(x=sil_avg, color="red", linestyle="--")

 

• 위의 visualization 함수를 사용하면 아래와 같은 차트를 얻을 수 있는데, (군집개수 리스트와 입력데이터를 인풋으로) 각 cluster안의 데이터별 실루엣 계수들을 오름차순으로 나열한 bar chart 모양이다. (y축 두께가 두꺼운건 클러스터는 소속 데이터 포인트가 많다는 것) 
• 아래 예시에서는, 전체 데이터의 실루엣평균 (빨간점선) 안에 균일하게 들어와있는 4개 cluster 케이스가 좋아보임 

visualize_silhouette([ 2, 3, 4, 5], X)