반응형
Index
Entropy
- 엔트로피(entropy)란, '정보를 표현하는데 필요한 최소 자원량 기대값' → 이걸 bits (0과1)로 표현
- 위키에서 표현한 엔트로피는 '각 메세지에 포함된 정보의 기대값' 혹은 불확실성이라고도 표현한다.
- 정보를 인코딩할 때 확률이 높은건 짧게, 확률이 낮은건 길게 코딩해서 정보를 최대한 적은량의 bits로 표현
- cf. 알다싶이 기대값은 확률×도수 이다. 엔트로피에서 도수는 자원량을 의미
- 엔트로피를 수식으로 표현하면 아래와 같다. 아래 수식의 기대값이 항상 최소값이라고 섀런이라는 사람이 증명함 (x가 continuous 하면 시그마는 ∫ , log는 ln으로 바뀜)
- - log 함수를 활용하여, 확률이 1에 가까울수록 도수가 0이 되고, 0에 가까울수록 1이 되는 모양

- 엔트로피는 p(x)의 분포가 uniform일때 가장크다 (최악이다). 엔트로피를 '불확실성' 이라고 표현할때가 많은데, 불확실성 관점에서 보면 uniform분포가 가장 불확실하고 그때 엔트로피가 가장크다. 반대로 앞면이 99%나오는 동전이 있다고 하면 불확실성이 매우 낮은, 즉 엔트로피가 매우 낮은 확률분포의 예시가 된다.
- 다시 정리하면 확률p에 대한 도수를 -log p 로했을때 기대값이 최소가 된다는 개념..
Cross-Entropy
- Cross-Entropy 는 Entropy 의 도수 부분을 실제 확률 p* 가 아닌 예측확률 p를 사용하는 것이다. 그렇기 때문에 entropy보다는 값이 크겠지 (entropy가 최소 기대값이라고 했으니)
- 그래서 예측 모델에서 실제값 부분이 P* 로, 예측값 부분이 P로 들어가는 CE를 쓰는것이다. 실제와 같을수록(크로스 엔트로피가 엔트로피에 다갈수록) 최소가 되니깐

KL-divergence
- Entropy 측면에서, 비효율적인 정도를 나타냄
- 정보 표현 측면에서, Entropy는 최고로 효율이 좋은 인코딩 Cross Entropy는 잘못코딩한것 (효율이 안좋은것)
- 따라서 KL-diverge 는 Cross Entropy - Entropy 이기 때문에 아래와 같은 수식이 나온다. = - p×log(q) + p×log(p) * 참고로 항상 Cross Entropy > Entropy 이다.
- 같은 말이지만 CE를 최소화 하는것이 KL을 최소화 하는것이다.

Mutual Information
- 아래 수식을 보면 KL divergence와 똑같다.
- 즉, 실제로는 p(x,y) : 독립이 아닌데 예측을 p(x),p(y) : 독립이라고 했을때의 KL divergence (비효율적인 양)
- 따라서 실제로 독립일수록 MI 값이 작다 (예측과 동일하니). 반대로 실제로 상관관계가 클수록 MI 값이 크다.

- 위 식을 분해하면 아래와 같이 entropy 표현식으로 해석할 수 있고. Y의 불확실성에서 X를 알고있을때 Y의 불확실성을 뺀 값이다. 따라서 최소일때는 독립인상황 즉 MI가 0일때 이다.

- 위 풀이과정에 빠진 한줄. I(X;Y) = H(X) + H(Y) - H(X,Y) 로도 표현 가능하다.
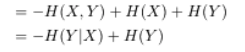
※ 왜 독립이면 P(x,y) = P(x) × P(y) 인가?
독립이면 P(x|y) = P(x)
P(x|y) = P(x,y) / P(y)
반응형
'Study > ML' 카테고리의 다른 글
| 고유값(eigenvalue) 고유벡터(eigenvector) (0) | 2023.07.04 |
|---|---|
| 예측모델 실습 (mercari제품가격 예측) (0) | 2023.06.22 |
| 12. 군집화(Clustering) (0) | 2023.06.05 |
| 11. 차원축소(PCA,LDA,SVD) (0) | 2023.06.01 |
| 10. 회귀(Regression) - 로지스틱 회귀, 회귀 트리 (0) | 2023.05.31 |




댓글