11. 차원축소(PCA,LDA,SVD)

Index

● 차원축소 개요 

차원의 저주(Curse of Dimensionality): 데이터의 차원이 너무 크면 모델을 학습하는데 여러가지 문제점이 있을수 있다.

• 데이터간의 거리가 기하적으로 멀어지며 희소(sparse)한 구조를 갖게된다. 따라서 데이터 거리기반의 알고리즘 (KNN, SVM)에 부적합해지며, 과적합의 위험성도 커지고 계산속도도 저하된다. 
• 피쳐가 많다는 의미는 그만큼 다중공선성(multi-collinearity) 문제가 발생할 경향이 크다. 

이러한 이유로 우리는 고차원 데이터에 대해, 전처리 과정 중 하나로 차원축소를 진행하는데, 방법은 크게 두가지이다. 

1. Feature Selection : 특정 피처에 종속성이 강한 불필요한 피처는 제거하고 독립적인 피처들만 선택
2. Feature Extraction : 기존 피처들을 저차원의 새로운 중요 피처(Latent Factor)들로 압축

이번 포스팅에서는 Feature Extraction 의 대표적인 모델들에 대해 정리한다. 

 

● PCA (Principle Component Analysis) : 주성분분석

◎ 직관적인 설명

1. Projection 했을 때 분산이 가장 큰 축을 PC1으로 설정, PC1의 Loading score(=기울기)를 구함

2. PC1에 직교하는 벡터 PC2로, 또 그에 수직인 벡터 PC3, PC4.. 생성

3. PC1,2,3,4 를 각 축으로 하는 scree plot 생성. y축은 eigenvalue 즉 각 PC축의 설명력을 나타낸다.

   오른쪽 아래 차트와같이 PC누적 설명력(녹색선)을 같이 표현하기도 한다. 

4. 각 PC의 설명력을 감안해 사용할 PC를 선택.

   예를들어 80%이상의 설명력 확보하려면 아래 예시 차트에서는 PC1,2 2차원까지 축소한다.

◎ 수학적인 설명

 1. 고차원 데이터의 피쳐간 covariance matrix(공분산행렬)를 구한다. 

 2. Covariance matrix의 Eigenvector(고유벡터)와 Eigenvalue(고유값)를 구한다. 

 3. Eigenvalue 값이 큰 순서대로 Eigenvector를 정렬한다. 

 4. 원하는 만큼의 Eigenvector를 사용하여 차원 축소를 진행한다. 

※ Eigenvector가 위의 직관적 설명에서의 PC1,2,3.. 축들이고 Eigenvalue가 screeplot 에서의 설명력에 대한 비율이다.

※ Eigenvector 는 n*n 정방행렬의 경우 n개 존재하며, 선형변환시에도 방향은 안변하고 크기만 변하는 벡터이다. 

 

◎ 코드 구현

- PCA를 적용하기 전에는 개별 피쳐들을 scaling 해주는게 중요하다. (cov등 여러 속성값을 계산해야하기 때문)

from sklearn.preprocessing import StandardScaler                                                                                          ↓ irisDF

# StandardScaler를 이용하여 표준 정규 분포를 가지는 값들로 변환

iris_scaled = StandardScaler().fit_transform(irisDF.iloc[:, :-1])

from sklearn.decomposition import PCA

pca = PCA(n_components=2)

                                                 

# fit( )과 transform( ) 을 호출하여 PCA 변환 데이터 반환                                                                          ↓ irisDF_pca 

pca.fit(iris_scaled)

iris_pca = pca.transform(iris_scaled)                                                      

print(iris_pca.shape)

 

pca_columns=['pca_component_1','pca_component_2']

irisDF_pca = pd.DataFrame(iris_pca, columns=pca_columns)

irisDF_pca['target']=iris.target

irisDF_pca.head(3) 

 

 

 

 

# 2개의 PCA축의 설명력을 plot 으로 시각화 및 설명력 출력함수 확인

plot_data(irisDF_pca, x='pca_component_1', y='pca_component_2')  

print(pca.explained_variance_ratio_)  # 출력결과 : [0.7296 0.2285]

 

 

 

 

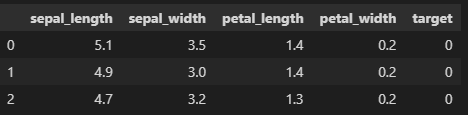
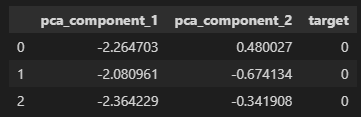
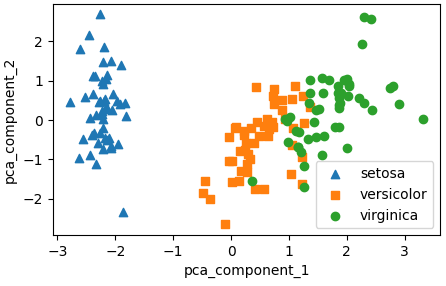
- 피쳐가 수십개 있을때 각 속성간에 상관관계를 먼저 탐색하고 (corr매서드 및 heatmap 시각화 활용) 상관관계가 높은 피쳐들을 중심으로 차원축소(PCA 한다). 아래 예시에서는 PAY_ 컬럼과 BILL_AMT 컬럼 들 간에 상관도가 높기에 이들을 중심으로 PCA 진행

import seaborn as sns

import matplotlib.pyplot as plt

corr = X_features.corr()

plt.figure(figsize=(8,8))

sns.heatmap(corr, annot=True, fmt='.1g')

 

● LDA (Linear Discriminant Analysis) : 선형 판별 분석법

•  PCA와 같이 저차원으로 projection 하는 기법이지만, LDA는 분류모델에서 사용하기 쉽도록 클래스를 분류할 수 있는 기준을 최대한 유지하면서 차원축소한다. 
• LDA는 입력 데이터의 결정 값 클래스를 최대한으로 분류할 수 있는 축을 찾는다. (PCA는 분산이 가장 큰 축) 아래 그림에서는 왼쪽보다 오른쪽 축이 LDA 측면에서 더 잘 projection한 축이다. 

• 클래스 간 분산(between) / 클래스 내부 분산(within)을 최대화하는 방식으로 차원을 축소한다. 
• PCA는 공분산 행렬에 대한 고유벡터를 구했다면, LDA는 클래스간 분산행렬 / 클래스 내부 분산행렬에 대한 고유벡터를 구하고 프로젝션한다. 
• PCA는 라벨이 필요없는 비지도학습 ↔ LDA는 라벨이 필요한 지도학습. 따라서 아래코드와 같이 target데이터를 함께 줘야한다. 

 lda = LinearDiscriminantAnalysis(n_components=2)

 lda.fit(iris_scaled, iris.target) # LDA fit호출할때(축을 찾을때) 피쳐,라벨 정보 둘다 줘야함

 iris_lda = lda.transform(iris_scaled) # LDA transform호출할때(차원 축소할때) 피쳐만 입력   

 print(iris_lda.shape)

 

● SVD (Linear Discriminant Analysis) : 특이값 분해 

• SVD 에 대한 정확한 이해를 위해 긴 설명이 필요하므로 설명이 매우 잘 되있는 아래 블로그를 참고한다. https://angeloyeo.github.io/2019/08/01/SVD.html
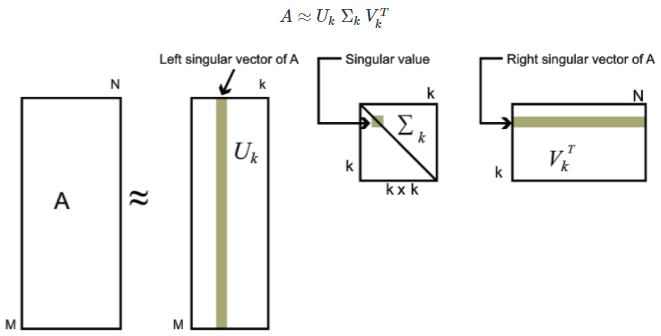
• SVD는 정방행렬이 아닌 n*m 크기 행렬을 분해
• U,V는 특이벡터행렬, Sigma(∑)는 대각행렬, 대각행렬의 0이 아닌값(k개)을 특이값으로 부른다. 
• SVD를 통해 변환된(차원축소) 데이터는, 원본 데이터를 분해해서 생긴 U*∑ 행렬에 선형변환을 해서 생성한다. 
• SVD는 데이터에 결측값이 많거나, 희소행렬에 대해 잘 동작한다. 

• 사이킷런의 TruncatedSVD 모듈을 활용한 SVD 구현 : Sigma에 있는 대각원소(특이값) 중에서도 상위 일부 데이터만 추출해서 분해하는 방식으로, 원본행렬을 정확히 원복하진 않지만, 추출을 많이 할수록 원본과 가깝게 복원한다. 

    from sklearn.decomposition import TruncatedSVD, PCA

    import matplotlib.pyplot as plt

    iris = load_iris()

    iris_ftrs = iris.data

    # 2개의 주요 component로 TruncatedSVD 변환

    tsvd = TruncatedSVD(n_components=2)

    tsvd.fit(iris_ftrs)

    iris_tsvd = tsvd.transform(iris_ftrs)

    # Scatter plot 2차원으로 TruncatedSVD 변환 된 데이터 표현. 

    plt.figure(figsize=(5,3))

    plt.scatter(x=iris_tsvd[:,0], y= iris_tsvd[:,1], c= iris.target)

    plt.xlabel('TruncatedSVD Component 1')

    plt.ylabel('TruncatedSVD Component 2')

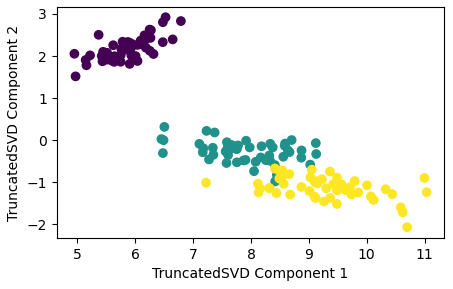
• 사실, 사이킷런의 PCA 와 SVD 모듈로 차원축소한 결과를 비교해보면 차이가 거의 없는데, PCA가 SVD 알고리즘으로 구현되었기 때문이고, 차이점은 PCA는 Dense Matrix 에 대해서만 변환가능하고, SVD는 Sparse Matrix에 대한 변환도 가능한 점이다.