반응형
고유값, 고유벡터란?
어떠한 행렬 A에 대해서, 그 행렬을 일종의 함수라고 생각했을때
- 해당 함수를 거쳐도 방향이 바뀌지 않고 크기만 바뀌는 어떠한 벡터가 eigencevtor 고유벡터이다.
- 반면 해당 벡터가 상수배 된다고 했을때, 그 상수값이 eigenvalue 고유값이다.

고유값, 고유벡터 구하기
고유값(eigenvalue)를 구하는 수식은 아래와 같다. (위에식을 정리한 같은 결과이다)
- 즉, A-λI 의 determinant 값이 0이 되게 하는 복수의 λ가 고유값(eigenvalue)이고,
- 이때 A-λI 의 영공간(Null space ; 곱해서 0이 되게 만드는 해)가 고유벡터(eigenvector)이다.
- 따라서 고유값은 여러개일 수 있고, 하나의 고유값에 고유벡터는 무한개이다 (특정한 벡터로 표현할때는 영공간의 기저로 표현한다)

고유값 분해 (eigen decomposition)
앞서 다룬 행렬 A의 고유값을 λi, 고유벡터를 vi, i = 1, 2,..., n이라고 하자.

고유벡터 집합을 열벡터로 하는 행렬 P로 전환하고, Λ는 고유값을 대각원소로 가지는 대각 행렬이라고 하면 아래와 같이 표현할 수 있다.

- 즉, 어떠한 (정방)행렬 A의 고유벡터 행렬(P)이 역행렬을 갖는다면 그 행렬A은 대각화 할 수 있다. 고유벡터 행렬(P)가 역행렬을 갖는다는건 고유벡터(v1,v2...)각각이 선형 독립이라는 뜻이다.
- 대각화 한다는것의 가장 큰 장점은 거듭제곱이 매우 쉽다.

대칭행렬의 특징
- 모든 대칭행렬 (예를들어 correlation matrix)는 실수인 고유값을 가지고, 고유벡터는 서로 직교(orthogonal)한다.
- 즉 고유벡터행렬 V의 전치행렬이 곧 역행렬이된다. (크기1로 정규화되었을때)
- 따라서 아래와 같이 역행렬 계산없이 고유값,고유벡터로 대각화를 할수있다.
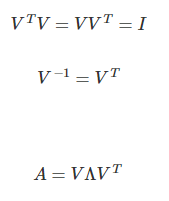
요약
N차원 정방행렬 A에 대해
- 행렬 A는 N개의 고윳값-고유벡터를 가진다(복소수인 경우와 중복인 경우를 포함).
- 행렬의 대각합은 모든 고윳값의 합과 같다.
- 행렬의 행렬식은 모든 고윳값의 곱과 같다.
- 행렬 A가 대칭행렬이면 N개의 실수 고윳값을 가지며 고유벡터들이 서로 **직교(orthogonal)**이다.
반응형
'Study > ML' 카테고리의 다른 글
| 정보이론 - 엔트로피, KL-divergence, Mutual Information (1) | 2023.07.04 |
|---|---|
| 예측모델 실습 (mercari제품가격 예측) (0) | 2023.06.22 |
| 12. 군집화(Clustering) (0) | 2023.06.05 |
| 11. 차원축소(PCA,LDA,SVD) (0) | 2023.06.01 |
| 10. 회귀(Regression) - 로지스틱 회귀, 회귀 트리 (0) | 2023.05.31 |




댓글