반응형
시계열 클러스터링은 시간에 따른 데이터의 패턴을 기반으로 여러 시계열 데이터를 그룹화한다. 각 시계열은 유사한 패턴, 트렌드, 계절성 등을 기준으로 클러스터에 속하게 되는데, 이를 통해 데이터의 구조를 이해하고, 예측 모델의 성능을 향상할 수 있습니다. 우리가 클러스터링을 할 때는 주로 거리나 밀도를 기반으로 유사도(similarity)를 측정하게 되는데, 시계열 데이터의 경우 주로 동적 시간 왜곡(DTW : Dinamic Time Warping)이라는 거리 측정 방법을 사용한다.
DTW는 아래의 그림과 같이 시계열 데이터간의 길이나 크기가 달라도 이것을 고려하여 유사성을 측정하는 방법이다. 두 시계열의 각 지점 간의 유클리디언 거리를 기반으로 거리 행렬을 만들고, 최적 경로 (최소 누적거리)를 찾는 방식으로 유사성을 평가한다.
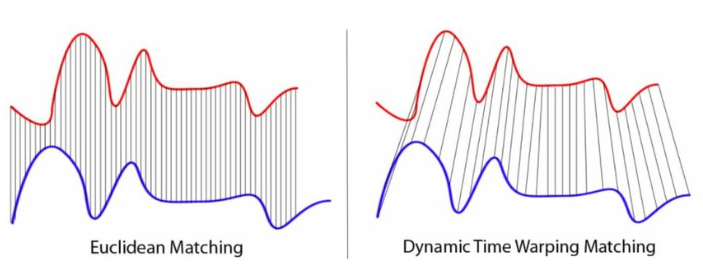
아래서부터는 시계열 데이터를 DTW 기반으로 클러스터링 하는 예제 코드이다.
시계열 데이터 전처리
- 시계열 데이터의 전처리와 클러스터링을 위한 모듈 설치 및 실행
! pip install tsmoothie # 시계열 관측치 스무딩
! pip install tslearn # DTW 이용한 시계열 클러스터링
from tsmoothie.smoother import *
from tslearn.clustering import TimeSeriesKMeans
from tslearn.preprocessing import TimeSeriesScalerMinMax- 시계열 데이터의 클러스터링을 위해 슬라이딩 윈도 형식으로 데이터를 변환해 준다.
- 아래 코드는 tsmoothie.smoother 의 WindowWrapper를 이용하여 윈도 슬라이딩과 스무딩을 동시에 실행한다.
## Smooth price series
window_shape = 20
smoother = WindowWrapper(LowessSmoother(smooth_fraction=0.6, iterations=1), window_shape=window_shape) # LOWESS(Locally Weighted Scatterplot Smoothing)
smoother.smooth(df_close.loc['AMZN'])
low, up = smoother.get_intervals('prediction_interval') # only for visualization
- 슬라이딩 윈도우와, 스무딩 결괏값 반환은 아래와 같이 할 수 있다.
print(smoother.Smoother.data) # 슬라이딩 윈도우 결과만 반환
print(smoother.Smoother.smooth_data) # 슬라이딩 윈도우 후 스무딩까지한 결과 반환
- 클러스터링은 결국 distance 기반이기 때문에 데이터 간에 스케일을 맞추어 주는 게 필수적이다. (특히 시계열에선)
## Scale price series - raw data
raw_scaled = TimeSeriesScalerMinMax().fit_transform(smoother.Smoother.data)
시계열 데이터 클러스터링
- DTW 기반 K-means 모델 생성 학습 및 결과(군집 라벨 및 중심점) 출력
## Make clusters using raw price series
## DTW(Dynamic Time Warping)
kmeans_raw = TimeSeriesKMeans(n_clusters=4, metric="dtw", max_iter=10, random_state=123) ###
kmeans_raw.fit(raw_scaled)print(kmeans_raw.labels_)
print(kmeans_raw.cluster_centers_)
- 군집결과 시각화. 군집별 소속된 시계열 데이터들과 군집 중앙점을 그래프로 표현
### Visualize price series clusters
colors = {0:'orange',1:'green',2:'blue',3:'red'}
for c in range(kmeans_raw.n_clusters):
plt.figure(figsize=(5,3))
plt.plot(np.squeeze(raw_scaled[kmeans_raw.labels_ == c],-1).T, c=colors[c], alpha=0.03)
plt.plot(np.squeeze(kmeans_raw.cluster_centers_, -1)[c], c=colors[c], linewidth=3)
plt.title(f"Time Series Cluster #{c}")
plt.show()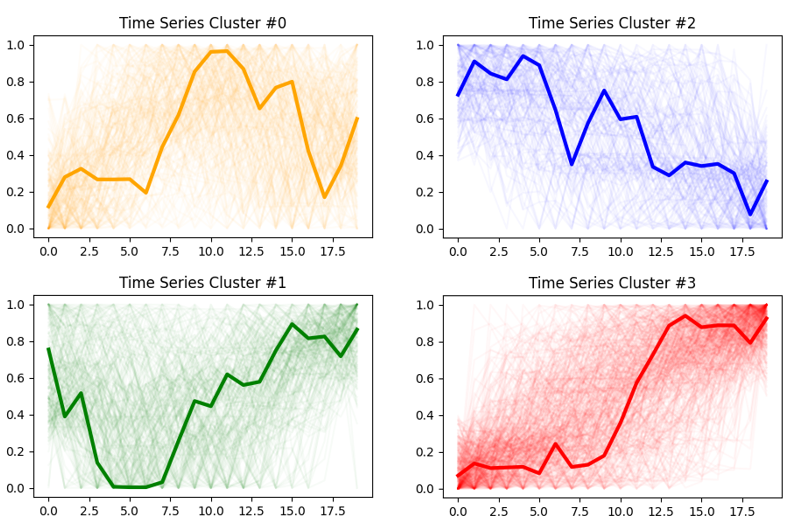
- 전체 시계열 데이터의 군집 분포 시각화
### Visualize price series clusters
plt.figure(figsize=(10,5))
plt.plot(smoother.Smoother.data[:,-1], c='black', alpha=0.3)
plt.scatter(range(len(smoother.Smoother.data[:,-1])), smoother.Smoother.data[:,-1],
c=[colors[c] for c in kmeans_raw.labels_])
plt.xticks(range(0,len(df.timestamp.unique())-window_shape, 100),df.timestamp.dt.date.unique()[window_shape::100])
plt.ylabel('AMZN Price')
plt.title("Time Series Clustering - Phase Detection in Stock Market (Raw)")
plt.show()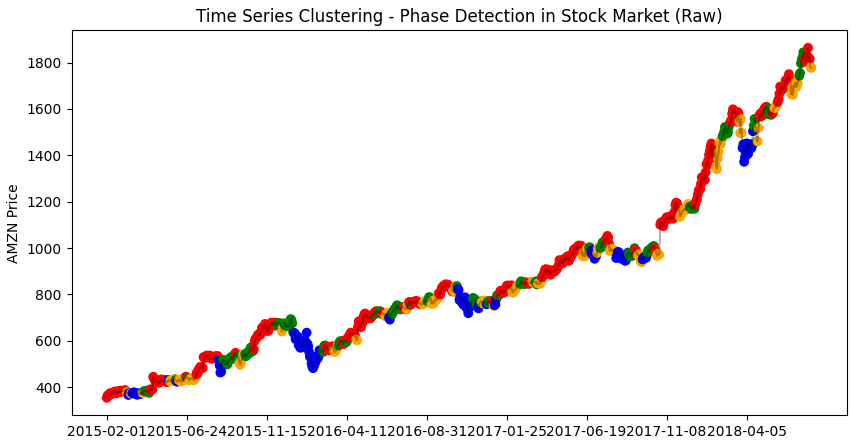
반응형
'Study > 시계열' 카테고리의 다른 글
| 8. (Transformer-2편) Transormer : Self-Attention (0) | 2024.07.24 |
|---|---|
| 7. (Transformer-1편) RNN 과 Attention (1) | 2024.07.24 |
| 5. Seq2Seq 모델을 이용한 다변량 다중시점 시계열 예측 (1) | 2024.07.08 |
| 4. Prophet 패키지를 이용한 간단 시계열 예측 (0) | 2024.07.08 |
| 3. 딥러닝을 이용한 시계열 예측 (TensorFlow, LSTM) (1) | 2024.07.08 |




댓글