반응형
시계열 분석을 위한 확률모형
- 시계열 분석을 위한 확률모형은 데이터의 시간적 패턴 (추세변동, 계절변동 등)과 변동을 설명하는 통계적 방법
- 확률 모형이 시계열 데이터를 잘 추정했을 때 '잔차 시계열 자료 (residual error series) ' 는 백색잡음(white noise) 이 되어 서로 독립적이고 일정한 분산을 갖는다. (대게 정규분포를 따른다)
- 이러한 컨셉에서 출발한 확률 모형들이 대표적으로 AR, MA, ARIMA, SARIMAX, VAR, ECM 등이 있다.
- 확률모형의 분석은 4단계로 진행된다 : Box-Jenkins 방법론
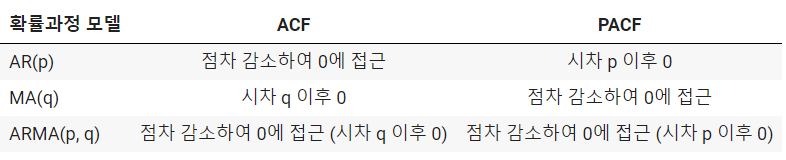
- 모형 설정 (Model Identification) : ACF, PACF 와 같은 지표, 혹은 auto.arima 와 같은 프로그램을 이용하여 시계열 자료에 '적합한' 확률모형을 선택한다 (AR/ARIMA/VAR 등 중에서 어떤 모형을 쓸지).
- 모수 추정 (Parameter Estimation) : 설정한 모형에 따라 모수를 추정하고 적합성을 검토한다. 즉, 확률모형을 통한 시계열 예측은 특정한 모형을 가정한 뒤 파라미터를 찾는 '모수추정방식' 이다.
- 분석 결과의 검정(Statistical Testing) : 모형 적합도에 따른 잔차의 정상성과 분석결과 검정을 수행
- 예측(Forecasting) : 시계열 자료와 분석모형을 토대로 미래값을 예측
자기상관 함수
- 동일한 변수의 시점에 따른 상관관계를 측정하는 함수이다.
- ACF 값을 통해 시계열 자료의 정상성을 파악한다. 정상 시계열의 경우 급격하게 0으로 빠르게 떨어지고, 비정상 시계열은 천천히 떨어진다.
- PCAF 는 비교하고자 하는 두시점외의 모든 변수의 영향을 제거한 상태에서 순수한 상관계수를 측정함
- 시계열 데이터의 정상성 여부는 ACF 와 PCAF 값이 특정 신뢰한계 범위 안에 존재하는지로 판단함
- ACF 와 PACF 의 목적은? 시계열 자료의 자기상관성 및 정상성을 판단하여 → 확률모형(ARIMA) 의 차수(p,d,q)를 선택하기 위함
- 시계열 데이터의 정상성만 간단히 검증하는 ADF 테스트와는 목적이 다르다고 할수있음
※ ACF, PACF 테스트 진행 및 시각화 코드 예시
# ACF and PACF
from statsmodels.tsa.stattools import acf, pacf
lag_acf = acf(ts_diff, nlags=20)
lag_pacf = pacf(ts_diff, nlags=20, method='ols')
# ACF
plt.figure(figsize=(10,4))
plt.subplot(121)
plt.plot(lag_acf)
plt.axhline(y=0,linestyle='--',color='gray')
plt.axhline(y=-1.96/np.sqrt(len(ts_diff)),linestyle='--',color='gray')
plt.axhline(y=1.96/np.sqrt(len(ts_diff)),linestyle='--',color='gray')
plt.title('Autocorrelation Function')
# PACF 도 동일한 코드로 진행
안정 시계열 - AR, MA, ARMA
- 자기회귀모델 (AR, AutoRegressive Model)
- 변수 자기 자신의 과거값의 선형 조합으로 미래/현재 시점을 예측함
- AR(p) : p차 자기회귀 모형, ε 은 평균이 0이고 분산이 1인 정규분포 따르는 백색잡음
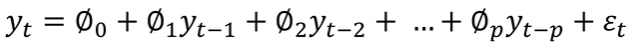
- 이동평균 (MA, Moving Average)
- 과거시점의 예측 오차를 이용하여 미래/현재 시점을 예측함
- MA(q) : q차 이동평균 모형

- 자기회귀 이동평균 (ARMA)
- 위에 두가지 모델을 합친 모형
- ARMA(1,1) = AR(1) + MA(1) : 가장 흔하게 쓰이는 차수. 차수가 올라간다고 결코 좋은건 아님

불안정 시계열 - ARIMA
- 앞선 AR, MA, ARMA 모델을 사용하기 위해서는 시계열 데이터가 정상(stationary)상태여야한다. 그런데, 대부분의 시계열 데이터는 non-stationary 하다.
- 따라서 비정상 시계열을 '차분'을 통해 stationary하게 바꿔준 뒤 ARMA 를 적용하는 방식이 ARIMA 이다.
- ARIMA(p, d, q) : d차 차분한 데이터에 AR(p) 모형과 MA(q) 모형을 합친 모형
- p, d, q 값은 AIC/BIC (AIC/BIC 는 낮을수록 좋다), ACF/PACF 그리고 경험적인 자기상관 등 다양한 방법을 통해서 선택할 수 있다.
- 일반적으로는 ACF 와 PACF 그래프를 그려서 자기상관을 확인하고, 적합한 ARIMA 모형을 가정할 수 있다. 위의 ACF/PACF 그래프 예시로 돌아가보면, PCAF 를 통해 p =6 , ACF 를 통해 p=3 으로 정해볼 수 있다.
※ ARIMA 라이브러리를 통한 피팅과 예측 코드 예시
# ARIMA LİBRARY
from statsmodels.tsa.arima.model import ARIMA
from datetime import datetime
# fit model
model = ARIMA(ts, order=(1,0,1)) # (ARMA) = (1,0,1)
model_fit = model.fit()
# predict
start_index = datetime(1944, 6, 25)
end_index = datetime(1945, 5, 31)
forecast = model_fit.predict(start=start_index, end=end_index) # start=start_index, end=end_index
# forecast 값과, 기존데이터(ts) 를 이용해 시각화 비교 및 MSE, MAPE 등의 지표를 통한 오차 측정 가능함.
- 사실 현업에서 사용한다면 위의 과정들을 생략하고 Auto ARIMA 라이브러리를 활용하면 편하다.
! pip install pmdarima # Auto ARIMA 를 사용하기 위한 라이브러리
import pmdarima as pm
from pmdarima.arima import ndiffs
- 아래와 같이 ndiffs 함수를 사용하여 필요한 차분의 횟수를 구할 수 있다.
ndiffs(y_train, alpha=0.05, test='kpss', max_d=6)
ndiffs(y_train, alpha=0.05, test='adf', max_d=6)
- Auto ARIMA 를 활용하여 arima 모델을 생성하고 피팅하는 방법은 아래오 같다. ARIMA (0,1,0) 모형이 AIC점수가 제일 낮아 best model 로 선정되었음을 알 수 있다.
model = pm.auto_arima(y = y_train # 데이터
, d = 1 # (d)차분 차수 (기본값 = none), 지정하지 않으면 실행 기간이 매우 길어질 수 있음
, start_p = 0 # (p)탐색 시초값 (기본값 = 2)
, max_p = 3 # (기본값 = 5)
, start_q = 0 # (q)탐색 시초값 (기본값 = 2)
, max_q = 3 # (기본값 = 5)
, m = 1 # (기본값 = 1)
, seasonal = False # 기본값 = True, 계절변동 ARIMA(SARIMA)에 해당시 True로 수정
, stepwise = True
, trace=True # stepwise로 모델을 적합할 때마다 결과를 프린트
)
model.fit(y_train)
''' 결과 예시
Performing stepwise search to minimize aic
ARIMA(2,1,2)(0,0,0)[0] intercept : AIC=inf, Time=1.18 sec
ARIMA(0,1,0)(0,0,0)[0] intercept : AIC=632.062, Time=0.03 sec
ARIMA(1,1,0)(0,0,0)[0] intercept : AIC=633.161, Time=0.08 sec
ARIMA(0,1,1)(0,0,0)[0] intercept : AIC=632.943, Time=0.11 sec
ARIMA(0,1,0)(0,0,0)[0] : AIC=630.345, Time=0.05 sec
ARIMA(1,1,1)(0,0,0)[0] intercept : AIC=633.865, Time=0.35 sec
Best model: ARIMA(0,1,0)(0,0,0)[0]
Total fit time: 1.829 seconds '''
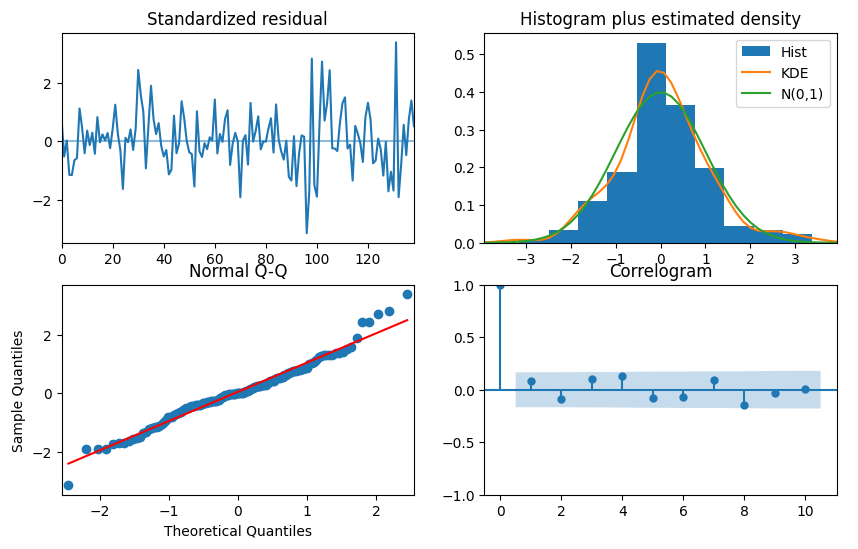
- 피팅된 ARIMA 모델의 결과는 model.summary() 를 통해 표로 볼 수 도 있지만, 아래와 같이 시각화해서 볼 수 있다.
- 1번 플랏 = 잔차의 정상성. 모델을 피팅한 뒤엔 항상 처음으로 잔차의 정상성을 확인해야한다.
- 2,3번 플랏 = 잔차가 정규분포와 얼마나 비슷한지.. skew 와 kurtosis 가 어느정도 있는것은 괜찮다. 시계열 데이터의 특징
- 4번 플랏 = ACF 그래프
model.plot_diagnostics(figsize=(10, 6))
다변량 예측모형
- 앞서 이야기한 ARIMA 까지는, 단변량 예측모델을 기준으로 한다.
- 다변량 예측모델을 위해서는 인풋 시계열 데이터를 vector 의 형태로 넣어줘야한다.
- 벡터자기회귀(Vector AutoRegressive Model, VAR) 은 k개의 AR식을 벡터로 쌓은것과 같은 모형이다.
- 두개 이상의 시계열 데이터가 공적분(Co-integration : 두 비정상 시계열을 선형조합했을 때 적분차수가 낮아지는 경우, 적분차수 = 정상 데이터로 만들기 위해 차분 필요한 횟수) 관계에 있다면,벡터오차수정모형(Vector Autocorection Model, VECM) 모형이 선호되기도 한다.
반응형
'Study > 시계열' 카테고리의 다른 글
| 6. 시계열 데이터 클러스터링 (DTW, TimeSeriesKMeans) (0) | 2024.07.09 |
|---|---|
| 5. Seq2Seq 모델을 이용한 다변량 다중시점 시계열 예측 (1) | 2024.07.08 |
| 4. Prophet 패키지를 이용한 간단 시계열 예측 (0) | 2024.07.08 |
| 3. 딥러닝을 이용한 시계열 예측 (TensorFlow, LSTM) (1) | 2024.07.08 |
| 1. 시계열 데이터와 시계열 분석 (1) | 2024.06.24 |




댓글