반응형
통계적 가설검정
우선 시계열 데이터 분석에 앞서 추후 시계열 데이터와 예측모델의 검정을 위해 '통계적 가설 검정'을 짧게만 복습해 보면...
- 유의 수준 (significant level, α) 이란? 평균으로부터 얼마나 떨어져 있어야 귀무가설(H0)을 기각할지. 유의 수준 99% 라는 것은, 정규분포의 1% 영역까지 떨어져 있어야 기각하겠다는 뜻.
- P-value 란? 유의 수준과 비교할 대상. 표본(sample)을 뽑았을 때, 그 샘플들의 결과보다 더 극단적인 결과를 얻을 확률. 예를 들어,, "여학생 평균키가 165cm 다" 를 귀무가설로, 샘플30명을 뽑아 평균을 내봤더니 170cm이다. 이 값에 대한 P-value가 0.01 이라는것은, 평균이 170cm보다 극단적인(큰) 샘플을 뽑을 확률이 0.01 밖에 안된다. 그렇기 때문에 내가 1% 확률을 뽑았을리가 없기 때문에 귀무가설을 기각하게 된다 (= 내가 가정한 H0라는 분포가 틀렸을 거다!)..
즉 P-value 가 유의 수준 α 보다 작거나, Test statistic (검정 통계량) 이 critical value 보다 크다면 H0를 기각한다.
시계열 데이터의 특징
- 기본적으로 자기 상관(autocorrelation)이 매우 강하다. 즉, 데이터끼리 전혀 i.i.d 하지가 않다. 시계열에서 'auto' 라는 단어는 self를 의미한다.
- 데이터에 펑크가 많다. 시계열 데이터 자체가 같은 시간 간격을 가정하는데, 매 같은 간격마다 모든 데이터가 수집되기는 현실적으로 어렵기 때문이다.
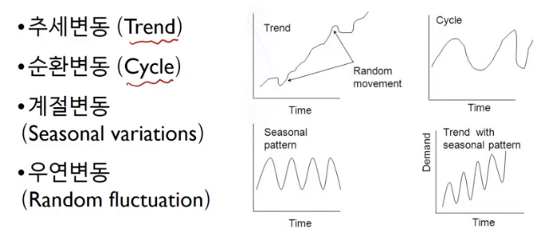
- 시계열 데이터는 크게 4가지 변동으로 구성된다. 추세(Trend) , 순환(Cycle), 계정(Seasonal), 우연(Random)
- 이러한 변동은 전처리 단계에서 먼저, 시각화를 통해 파악해 보고, 그 이후 요소분해(decomposition)를 포함한 필요한 전처리를 진행하게 된다.
- 정상(stationary) 시계열이란? 시점에 따라 평균과 분산이 변하지 않고, 공분산이 시차에 의해서만 의존하는 경우 (시점에 의존하지 않음) : 시점 t와 t+k 사이의 공분산을 함수로 보면 r(k) 다 t 자체는 영향을 주지 않는다.
- 정상성을 확인하기 위한 검정 방법
- 단위근(Unit Root) 존재여부 검정 : 단위근이란 시계열 데이터에서 자기회귀 모형(AR 모형) 중에서 계수 값이 1인 경우, 포착하고자 하는 데이터의 내재적인 특징.
- KPSS(Kwiatkowski-Phillips-Schmidt-Shin Test) 검정: (H0) 단위근이 존재하지 않을 것이다.
- ADF(Augemented Dickey-Fullter Test) 검정: (H0) 단위근이 존재할 것이다.
- 단위근(Unit Root) 존재여부 검정 : 단위근이란 시계열 데이터에서 자기회귀 모형(AR 모형) 중에서 계수 값이 1인 경우, 포착하고자 하는 데이터의 내재적인 특징.
- 등분산성(↔ 이분산성, Heteroskedasticity) : 시점에 따라 분산이 동일하다는것. 시계열 데이터는 등분산성이 충족되지 않고 시간이 지남에 따라 분산이 커지는 경우가 많다.
※ ADF 검증 예시 코드
# adfuller library
from statsmodels.tsa.stattools import adfuller
# Check adfuller
def check_adfuller(ts):
# Dickey-Fuller test
result = adfuller(ts, autolag='AIC')
print('Test statistic: ' , result[0])
print('p-value: ' ,result[1])
print('Critical Values:' ,result[4])
차분(Difference)
- 먼저 시차(lag)란, 예측시점과 예측을 위해 활용/참조하는 특정 과거 시점과의 시간차이이다.
- 차분(Differencing)을 한다는 것은, 추세를 제거하여 데이터가 정상성(stationarity)을 갖도록, 데이터를 시차 단위로 차이값을 계산하는 것을 말한다.
- 역차분(Inverse Difference)란? 모델링이 끝난 뒤에는 차분 데이터를 원시계열로 복원을 하기 위한 과정. 우리가 일반 데이터를 정규화하고 원복 하거나, 인코딩하고 디코딩하는 것처럼. 시계열은 자기상관성을 없애고 정상 시계열로 만들기 위해 차분을 하고, 역차분을 해주는 개념.

시계열 데이터의 EDA
- 대표적으로 스무딩(smoothing)과 필터링(filtering) 방법이 있다.
- 시계열 데이터는 크게 시간(time) domain과 주파수(frequency) domain으로 나눠볼 수 있다. 시간 도메인은, 시간축이 동일 간격의 discrete 한 값이다 (일별 주가 데이터처럼). 주파수 도메인은, 시간축이 연속적인 값이다 (라디오 주파수, 설비의 진동 데이터 처럼). 일반적으로 스무딩은 시간 데이터에서, 필터링은 주파수 데이터에서 많이 사용된다.
- 이동평균(Moving Average)은, 사전에 정해놓은 크기로 말 그대로 움직이면서 평균을 구하는 방식이다. 주식차트의 30일, 60일 이평선을 생각하면 된다. 윈도크기 (window size)가 클수록 더 스무드 해진다.
- 단순평균을 하면 단순 이동평균 (SMA, Simple MA)이고, 윈도 내에서 최근 데이터에 더 많은 가중치를 주면 지수 이동평균 (EMA, Exponentail MA) 혹은 가중 이동평균 (Weighted MA)이다.
- 이중 이동평균 (Double Moving Average) 은, 이동평균의 결과에 한번 던 MA 방식으로 스무딩 한 것이다. 아래 그림처럼 스무딩을 여러 번 할수록 더 스무드 해지고, 평균에 가까워진다.

※ 이동평균 시각화 코드 예시
# Check mean & std
def check_mean_std(ts):
# Rolling statistics
rolmean = ts.rolling(6).mean()
rolstd = ts.rolling(6).std()
plt.figure(figsize=(12,4))
orig = plt.plot(ts, color='red',label='Original')
mean = plt.plot(rolmean, color='black', label='Rolling Mean')
std = plt.plot(rolstd, color='green', label = 'Rolling Std')
plt.xlabel("Date")
plt.ylabel("Mean Temperature")
plt.title('Rolling Mean & Standard Deviation')
plt.legend()
plt.show()
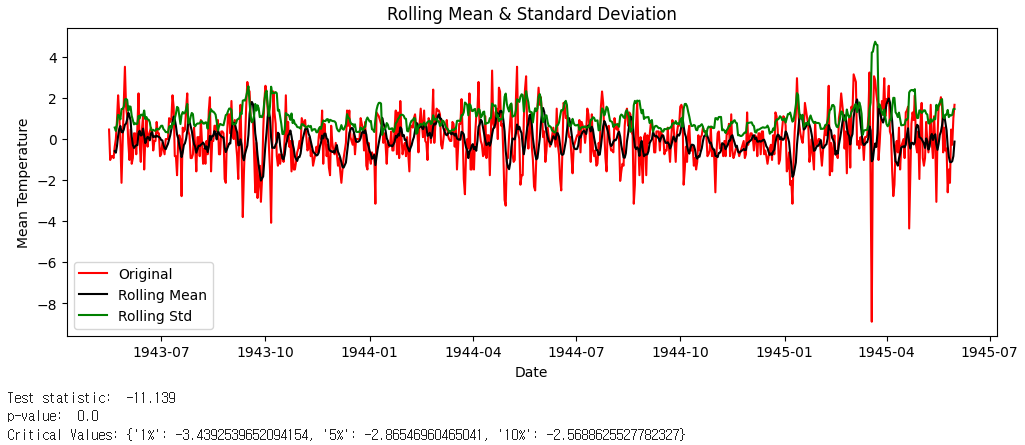
※ 이동평균 값을 차분한 뒤 차분결과 시각화 및 ADF 테스트
ts_moving_avg_diff = ts - moving_avg
ts_moving_avg_diff.dropna(inplace=True) # first 6 is nan value due to window size
# check stationary: mean, variance(std)and adfuller test
check_mean_std(ts_moving_avg_diff)
check_adfuller(ts_moving_avg_diff.MeanTemp)
- 추세나, 계절성을 제거한 시계열 데이터, 혹은 예측모델의 잔차 시계열 데이터의 정규성을 검증하기 위해서는 scipy 모듈을 통해 기술 통계량을 확인하거나 (외도 : skewness, 첨도 : kurtosis 확인), Q-Q plot 을 그려보는 방법이 있다.
- Q-Q plot 은, 두개의 분포가 동일한지를 검정하는데 한쪽은 일반적으로 정규분포이다. 즉, 정규성 검증 목적으로 사용한다. 두 데이터 분포의 각 분위수의 값을 비교하는 것이다.
- 예를들어, 아래 그림과 같이 정규분포를 따른다면 빨강선에 가까워야하는데 실제 분포(파란색)는 끝값일 수록 정규선과 많이 떨어져있다. 분위수가 3일때 가져야하는 값보다 실제 분포의 값이 훨씬 크다는 것의 의미는 => 꼬리가 더 두껍다는 의미이다 (Fat tail).
※ 시계열 데이터의 정규성 검증
import scipy.stats as scs
import statsmodels.api as sm
scs.describe(log_return)
# 결과 : DescribeResult(nobs=2061, minmax=(-0.1318402493393368, 0.08498951097376323), mean=0.0007197172841477838, variance=0.0002540709504954039, skewness=-0.23410408355207943, kurtosis=4.910552582890452)
# skew 는 0에 가까울수록 대칭적인데, 1을 넘어가면 매우 비대칭적. kurt 는 3이면 정규분포 정도.. 3보다 크면 뾰족
print("Skewness Test p-value: {:.7f}".format( scs.skewtest(log_return)[1]) ) # 샘플의 왜도가 정규분포와 일치하는지(0에 가까운 값을 가지는지 판단)
print("Kurtosis Test p-value: {:.7f}".format( scs.kurtosistest(log_return)[1]) ) # 샘플의 첨도가 정규분포와 일치하는지(0에 가까운 값을 가지는지 판단)
print("Normality Test p-value: {:.7f}".format( scs.normaltest(log_return)[1]) ) # 영가설: 샘플의 분포가 정규분포이다. (유의확률이 클수록 정규분포 가설을 강하게 지지)
sm.qqplot(log_return.flatten(), line='s')
plt.grid(True)
plt.xlabel("Theoretical Quantiles") # (정규분포 상의 이론적 분위수)
plt.ylabel("Sample Quantiles") # (샘플 분위수)
plt.title("Log Return Series Q-Q Plot") # 강한 fat-tail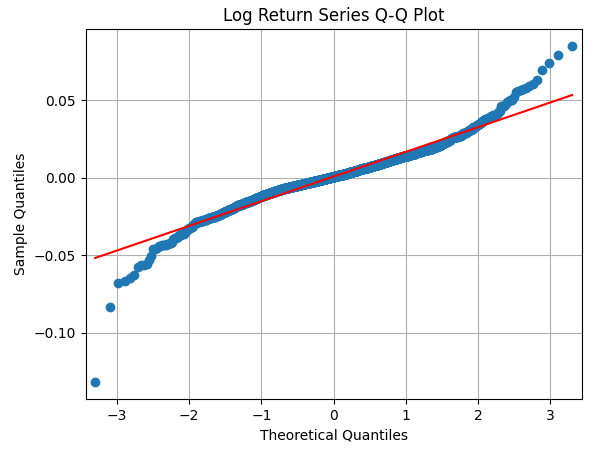
요소분해 (Decomposition)
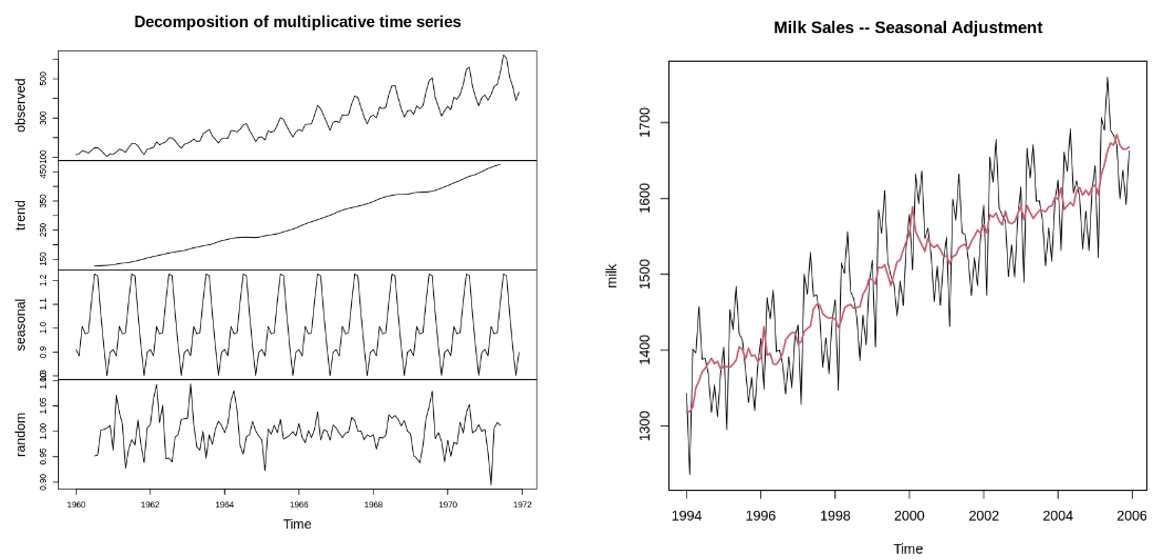
- 시계열 데이터의 여러 가지 변동 성분 (추세, 계절, 주기 등) 유무와 크기를 파악하기 위한 대표적 방법
- 수행 목적은? 추세와 주기 변동을 제거하고, 남은 잔차(residual) 시계열 자료를 우연변동에 의한 정상 시계열로 만들기 위함. 잔차(residual)는 white noise 가 돼야 한다. 일반 데이터의 정규화 과정과 같은 개념이다.
- 요소분해는 분해 방법에 따라, 선형적인 가법모형(Additive) 비선형적인 승법모형(Multiplicative)으로 구분된다.
반응형
'Study > 시계열' 카테고리의 다른 글
| 6. 시계열 데이터 클러스터링 (DTW, TimeSeriesKMeans) (0) | 2024.07.09 |
|---|---|
| 5. Seq2Seq 모델을 이용한 다변량 다중시점 시계열 예측 (1) | 2024.07.08 |
| 4. Prophet 패키지를 이용한 간단 시계열 예측 (0) | 2024.07.08 |
| 3. 딥러닝을 이용한 시계열 예측 (TensorFlow, LSTM) (1) | 2024.07.08 |
| 2. 시계열 분석을 위한 확률모형 (0) | 2024.06.26 |




댓글