반응형
Index
Cost function
- 인공지능 모델을 '학습'할때는 모델이 무엇이든 학습목적은 똑같다 : "목적함수(Objective function)을 최적화하는 Parameter를 찾는것" 이다. 그리고 이것은 일반적인 경우 비용함수(Cost function)을 최소화 하는 것이다.
- Cost는 Output(=실제값)과 Target(=예측값)간에 차이를 의미한다. 아래 그림은 분류문제의 예시이기 때문에 output의 값이 여러개이고 각output마다 cost를 따로 계산하여 더하는 모습이다.

- Cost function으로 주로 쓰이는 함수는 회귀문제의 경우 MSE,MAE,RMSE. 분류문제에서는 Cross-Entropy 손실함수가 주로 쓰인다.
- Cross-Entropy 함수는 아래 수식과 같이 실제값(y)=1 일때는 추정값(h)이 1에가까울수록 비용이 0이 되도록, y=0 일때는 h가 0에가까워야 비용이 0이 되도록 만들어졌다. 아래는 Binary label 문제 기준이지만, Multi label의 경우도 Cost계산을 위해 One-hot coding을 하기 때문에 결과는 동일하다.

Gradient Descent
- 앞서 모델학습의 목적은 "Cost를 최소화 하는 Parameter(θ)를 찾는 것" 이라고 했는데, Cost를 최소화 하기위한 방향(즉, 기울기)를 Gradient라고 한다. 수학적인 표현으로 Gradient는, 여러개 변수에 대한 편미분 값을 벡터로 정리한 것으로 아래 그림의 수식과 같이 표현된다.
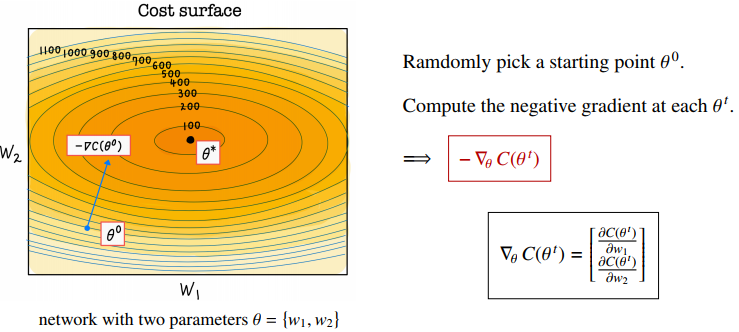
- C(θ)를 최소화 하기 위해 우리는 gradient를 negative 방향으로 "일정양" 만큼 update하는데 이것을 "gradient descent" (경사하강법)이라고 표현하고, update하는 양을 "learning rate(η)"라고 표현한다. (η는 하이퍼 파라미터)

Batch 와 Gradient
- Cost 와 Gradient 를 계산하는 단위가 "Batch"이다.
- batch, epoch, Iteration의 관계를 알아보면 1 epoch 의 의미는 데이터셋의 모든 데이터를 한번씩 학습하는것, batch size(혹은 mini batch)는 1 epoch을 학습할때 몇개 데이터씩 학습할지, Iteration은 최종 update횟수 이다. 예를들어 전체 데이터가 1,000,000개이고 batch size가 100개이면 1epoch에 Iteration은 10,000번이고 3 epoch을 학습하면 gradient update를 30,000번 하게 되는 의미이다.
- Gradient의 학습단위인 Batch의 크기를 1로 하기도 하고, 데이터셋의 크기만큼을 하는 방법도 있지만 대개의 경우 특정 사이즈(m)의 batch를 구성하여 batch단위로 gradient를 계산하고 parameter를 update한다. 그리고 이것을 Minibatch gradient Descent 혹은 Stochastic Gradient Descent (SGD) 라고한다.
반응형
'Study > DL' 카테고리의 다른 글
| CNN - 1편 (CNN의 구조) (0) | 2023.06.29 |
|---|---|
| Dropout 과 Batch Normalization (0) | 2023.06.29 |
| 활성화함수(Activation function)와 Optimizer (0) | 2023.06.29 |
| 역전파(Backpropagation)와 Vanishing gradient (0) | 2023.06.29 |
| Deep Neural Network, Perceptron, MLP (0) | 2023.06.28 |




댓글